ヴェレーナ新鎌ヶ谷　予定価格と間取り　モデルルーム訪問

今回ご紹介するのはヴェレーナ新鎌ヶ谷です！

［物件概要］　※記事作成時点での販売概要(第2期2次予定)

売主：大和地所レジデンス
施工：長谷工コーポレーション
価格：2400万円台・3200万円台
専有面積：70.76m²・72.59m²
総戸数：81戸
規模：地上7階
交通：北総線・成田スカイアクセス線・新京成線「新鎌ヶ谷」駅徒歩13分　東武アーバンパークライン「新鎌ヶ谷」駅徒歩14分　新京成線「北初富」駅徒歩2分
所在地：千葉県鎌ケ谷市東中沢一丁目
竣工:平成29年8月下旬

管理費（月額）12880円・13210円
修繕積立金（月額）6010円・6170円

駐輪場：162台（月額150円・200円）
駐車場：65台（月額1500円〜6900円）
サイクルポート：8区画（月額700円）

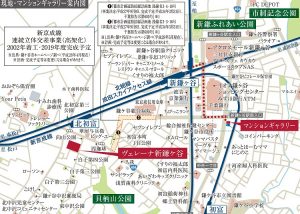
地図はこちらです↓

画像出典：ヴェレーナ新鎌ヶ谷公式HP

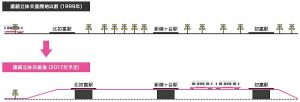
ヴェレーナ新鎌ヶ谷は新鎌ヶ谷駅の隣駅「北初富」から徒歩2分という好立地であることに加えて、新京成線の高架化工事、道路新設と将来性あるエリアに位置しています。現在は仮駅舎となっている北初富駅ですが高架化工事が順調に進んでおり平成31年度には北初富～初富間の高架化がすべて完了する予定となっています。

高架になれば12ヵ所の踏切がなくなるため464号お馴染みの大渋滞も緩和されます。八千代緑が丘に住んでいた頃は越谷レイクタウンなどへ行く際に車でよく通っていたのですが踏切がネックで渋滞していたことを思い出しました。

画像出典：新京成電鉄公式HP

それだけではなく道路も新設される予定がありますから現地から新鎌ヶ谷駅までも近くなる予定です。現状では新鎌ヶ谷駅までは遠回りするか仮設の歩道(歩行者のみ通行可)を通るため直線距離の割には遠く感じますがいずれは解消されます。

新鎌ヶ谷駅前にはアクロスモール、イオンなど買い物施設が充実していますが同マンションであれば新鎌ヶ谷駅周辺に依存することなく生活ができます。464号沿いにはスーパーも多くビッグ・エーまでは徒歩2分、オリンピックまでは徒歩5分と買い物至便です。

現地は通りから一歩中に入った住宅街のため静かな環境、さらにはバルコニー面は戸建が密集していますから眺望、採光が期待できる部屋が多くあります。

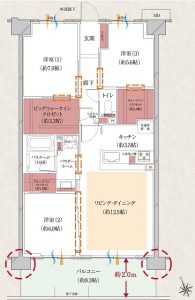
画像出典：ヴェレーナ新鎌ヶ谷公式HP

設備、仕様に関してはごくごく普通のものとなっていますが間取りは大和地所レジデンスお馴染みのオープンエアリビングを採用している住戸があります。

価格と間取りの一部を共有いたします。

C2bタイプ　80.92㎡　南西向き　3798万円　坪単価154万円

画像出典：ヴェレーナ新鎌ヶ谷公式HP

Iタイプ　80.45㎡　南東向き　3498万円　坪単価143万円

広告住戸では70.76㎡で2400万円台(予定)のお部屋もありますから目に優しい価格設定となっています。

周辺相場を確認しましょう！

モア・ステージ新鎌ヶ谷　1998年築　北初富駅徒歩2分　坪単価70万円程度
aieアクロスシティ　2007年築　北初富駅徒歩6分　坪単価80万円程度

上記の相場からヴェレーナ新鎌ヶ谷の将来価格を予想すると

C2bタイプ　80.92㎡　南西向き　3798万円(新築時)　→　1700万円(築20年時)

フルローンで購入した場合は20年後の残債が1700万円程度となりますから長期的に見れば大きな残債割れはないでしょう。ただエリア的に築浅時点ではフルローンでは残債割れの可能性が高くなりますから1割程度の頭金を入れておくと安心でしょう。

次に住むレーションです！

【新京成線→北総線】

北初富駅　7:59発
新鎌ヶ谷駅　8:00着　8:05発
日本橋駅　8:42着

【新京成線→JR常磐快速線】

北初富駅　7:37発
松戸駅　7:56着　8:03発
東京駅　8:33着

新鎌ヶ谷駅、松戸駅共に乗り換えは容易ですから大きなストレスなく都心通勤も可能です。思いのほか都心に近いエリアとなっています。新鎌ヶ谷駅からは新京成、北総(成田スカイアクセス)、東武アーバンパークラインが利用できますから将来的に職場移動があった際にも柔軟に対応できるでしょう。

【総評】

鎌ヶ谷市では約7年ぶりの新築マンション供給となります。【駅近】【買い物至便】【静かな住環境】【採光、眺望良好】【将来性】という魅力がありさらには目に優しい価格帯ですから安心しておすすめすることができます。とくに駅徒歩2分で静かな住環境という部分は現地で体感していただきたいところです。線路からも通りからも離れているのでものすごく静かです。近くには総合病院もありますからいざというときも心強いはずです。

懸念材料としては郊外あるあるの鉄道利用者減少で、実際に新京成電鉄では8両編成をすべて廃止してすべてを6両編成にしました。今後大きな人口増が期待できるエリアではありませんからワンマン運転化や駅の無人化などで経費削減をしていくことが予想できます。そこを気にしては郊外で家を買うことはできなくなってしまいますが頭の片隅には入れておいた方がいいでしょう。唯一の妥協点は沿線力であると考えます。